Selecting the Right Fan and the Importance of Fan Laws
Choosing the best fan is a mix of science and skill, requiring a deep understanding of multiple variables, options and alternatives.
The Fan Laws are one key, foundational element. Fan Laws demonstrate the relationship between the speed of rotation, the size of the fan, and the air density in the system. They calculate how changes to these variables impact airflow, power requirements and pressure.
All these interactions can be illustrated in a fan curve, which is a visual representation of the performance of a fan as per the Fan Laws. To learn more about fan curves, see our previous article on How to Read a Fan Curve.
To help explain how the Fan Laws work and how they are reflected in fan curves, we’ll start with the first three Fan Laws, where speed is the key variable. These three Fan Laws demonstrate how changes in speed will impact airflow (Fan Law #1), static pressure (Fan Law #2), and power requirements (Fan Law #3).
Fan Law #1: The Relationship of Fan Speed to Air Flow
This is the most straightforward of the Fan Laws. It states that the volume of air moved by a fan is directly proportional to the speed of a fan. In other words, doubling the speed of the fan will double the volume of air moved. Of course, there are limitations to speed, so other variables may need to be changed in order to achieve a given goal, but for the purposes of this explanation, we’ll keep everything else constant and look at the impact of increasing speed by a reasonable amount.
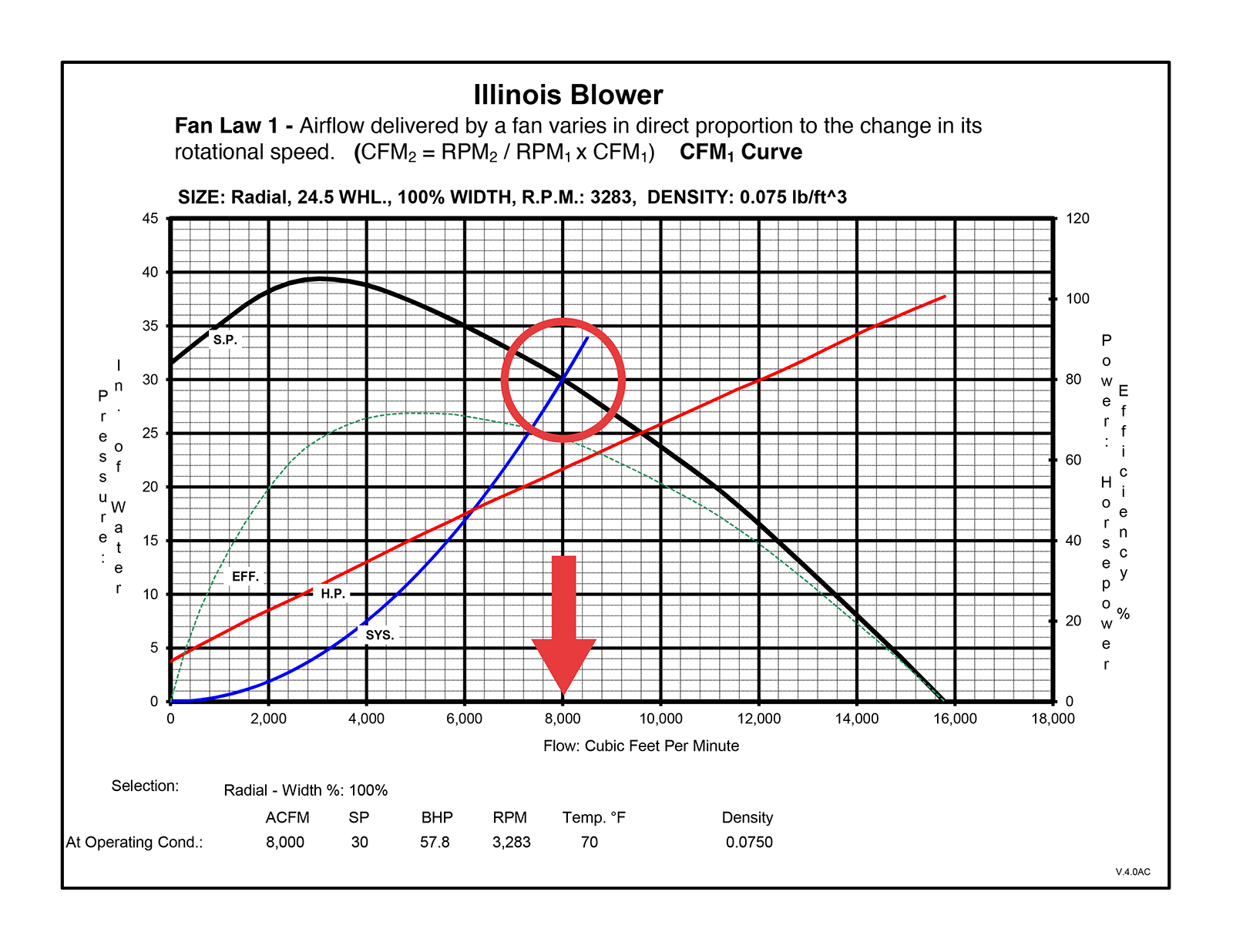
As you can see in the fan curve below, we have a fan with a 24.5” radial blade and an air density of .075 lb/ft. The rotational speed of the fan is set at 3,283 RPM.
The point where the S.P. and SYS lines intersect shows the maximum airflow in CFM. Drawing a line from this point to the bottom axis shows that this fan configuration will deliver an airflow of 8,000 CFM.
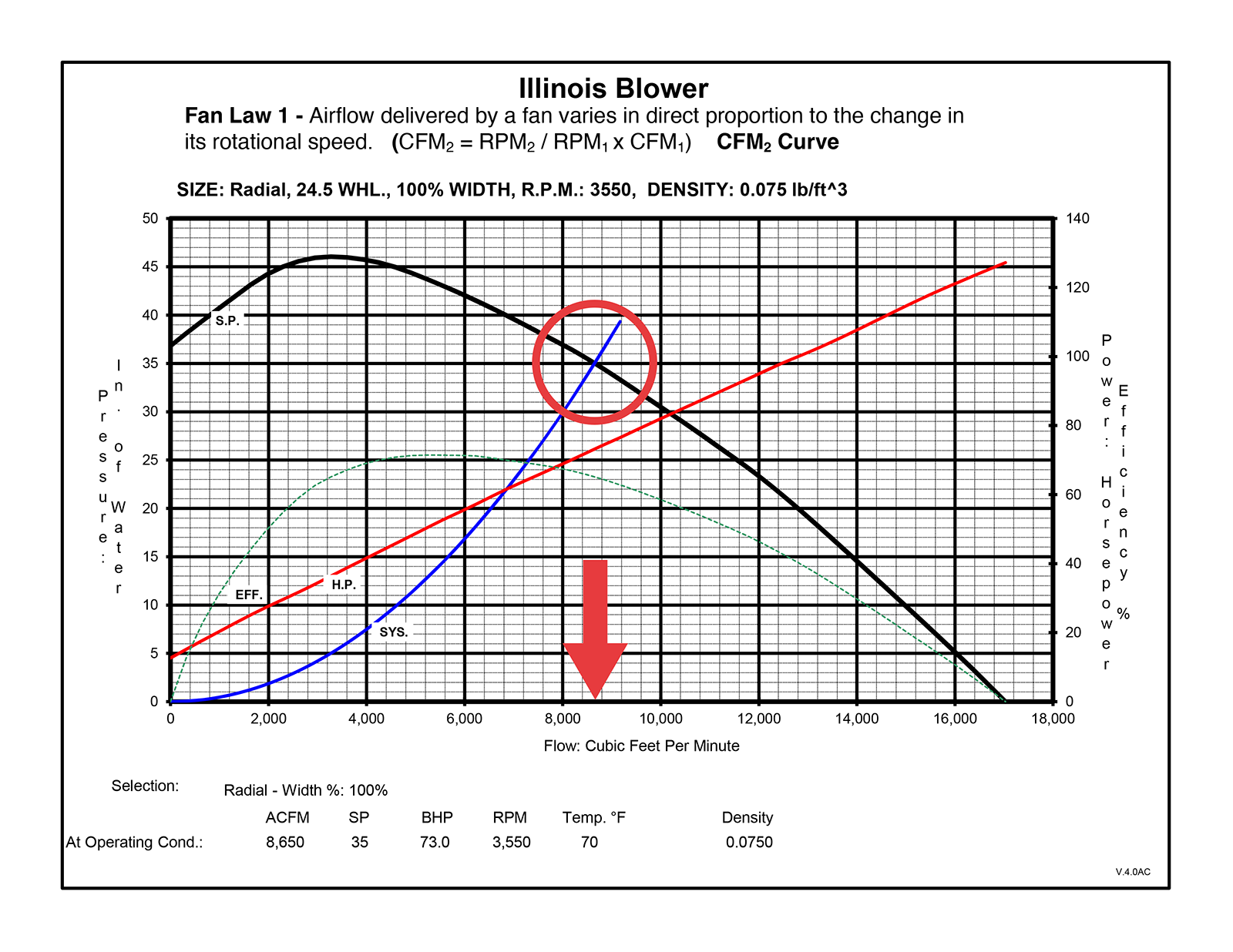
Now, let’s increase the speed of the fan from 3,283 RPM to 3,550 RPM (this is an increase of 8.13%).
Here, the S.P. and SYS lines have shifted to the right and now intersect at 8,650 CFM. The difference from 8,000 CFM to 8,650 CFM is an increase of 8.13%—the same percentage that the speed increased. Directly proportional, just as Fan Law #1 states.
Fan Law #2: The Relationship of Fan Speed to Static Pressure
As speed changes, the static pressure developed by the fan changes by the square of the change in speed. So, for example, if you double the speed, you quadruple the pressure.
Let’s revisit our initial fan curve showing a fan with a 24.5” radial blade, an air density of .075 lb/ft, and a speed of 3,283 RPM.
As this is the same fan curve as previously, the S.P. and SYS lines, of course, intersect at 8,000 CFM. Now, moving to the left axis, we see that the pressure is 30” of water (by the way, this is just above one psi).
So, let’s increase the speed of the same fan once again from 3,283 to 3,550 RPM (8.13%).
Now, the left axis indicates a pressure of 35” of water, an increase of 16.9%. As you can see, the 8.13% increase in speed created a 16.9% increase in pressure. (1.0813 squared = 1.169).
Fan Law #3: The Relationship of Fan Speed to Power Requirements
As speed changes, the power required changes by the cube of the change in speed. In this case, if you want to double the speed, you’ll need to increase the power by eight times.
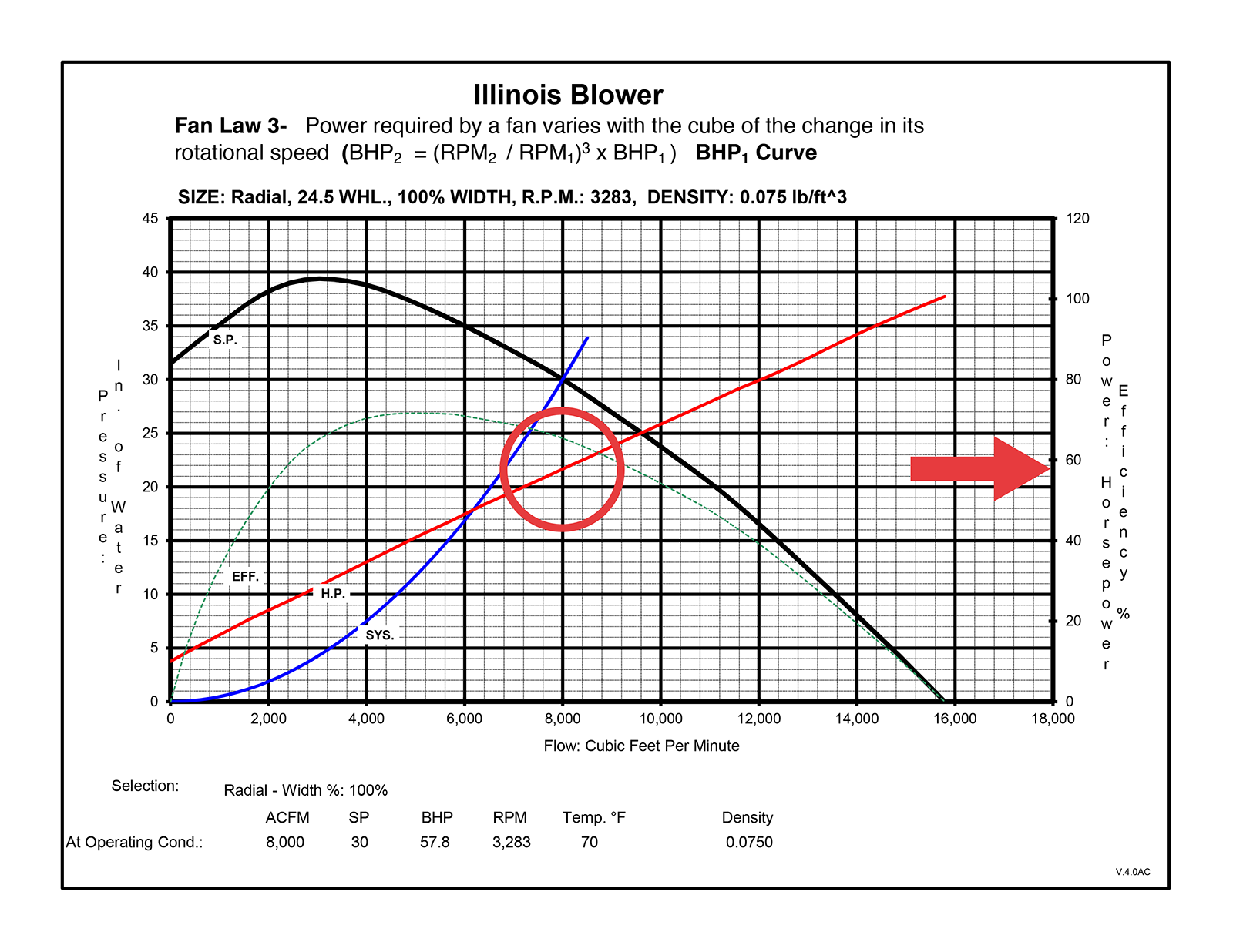
Back to our initial fan curve showing a fan with a 24.5” radial blade, an air density of .075 lb/ft, and a speed of 3,283 RPM.
Revisiting the point where the SYS and S.P. lines intersect (8,000 CPM flow), you’ll note that the red Horsepower line (H.P.) hits 8,000 CPM at 57.8 BHP (this measurement is on the right axis).
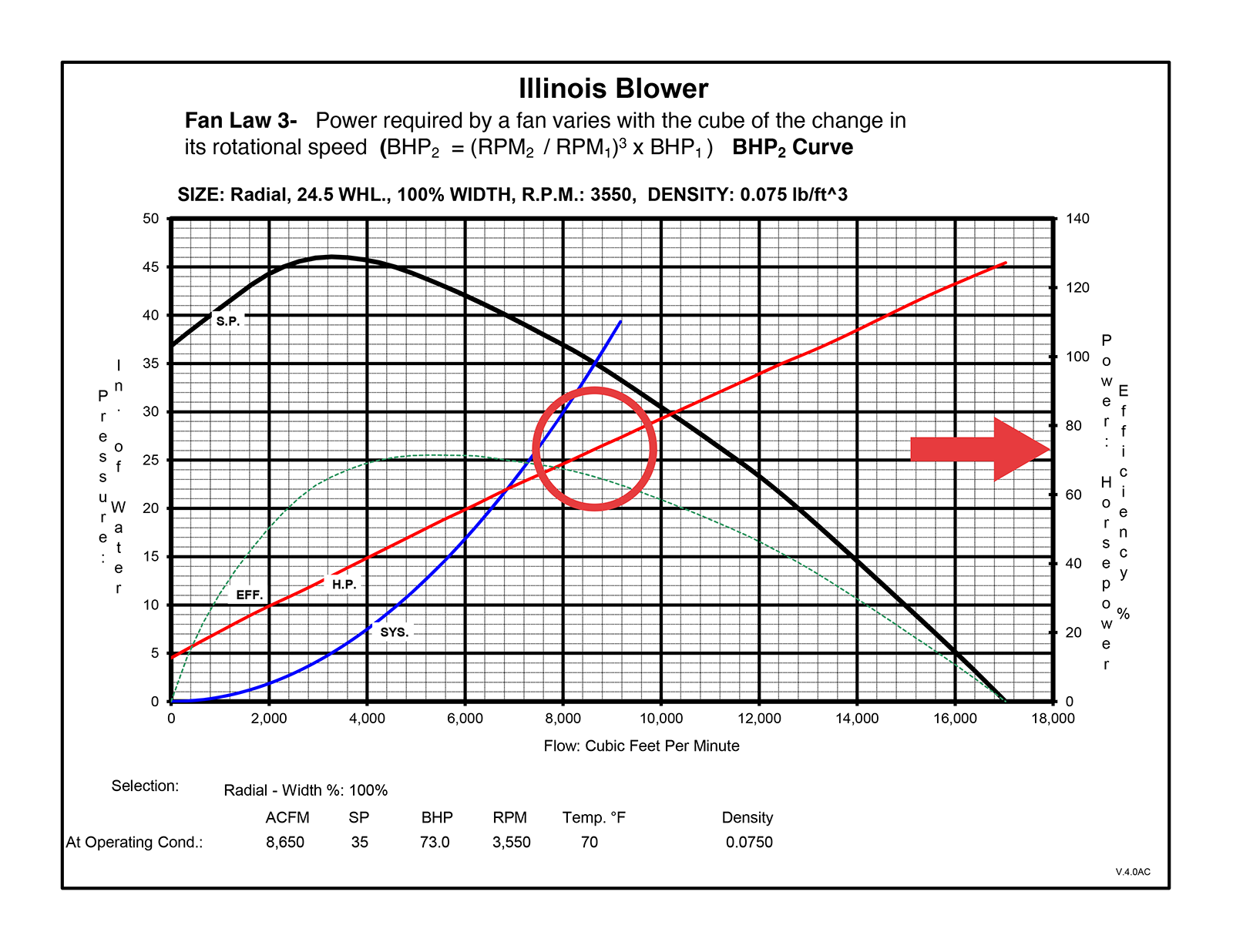
Once again, we’ll increase our speed specification by 8.13% to 3,550 RPM.
Now, the S.P. and SYS lines intersect at 8,650 Cubic Feet Per Minute, and tracking where the red line crosses this point (again, going to the right axis), shows a horsepower of 73.0 BHP.
The result? The 8.13% speed increase requires a horsepower increase from 57.8 to 73.0, or 26.4% (which is the increase in speed, cubed).
These are the most basic of the Fan Laws. They’re often called the “Three Fan Laws.” And as stated above, they illustrate what changes when speed is the key variable. However, other variables include fan size and air density, and these Fan Laws become more complex. All in all, Illinois Blower applies 12 Fan Laws in building the ideal solution.
Knowing Fan Laws is helpful, but no one relies on doing the math and hand-drawing fan curves. There are many software tools that can be applied, including our own fan selection software. Software can identify options, but knowledge, skill and experience are critical in finding the solution that will maximize reliability, provide superior performance, and minimize maintenance and service requirements. In some cases, the best answer also requires some creativity. For example, our team recently designed a daisy-chained dual-fan solution to best meet a particularly challenging requirement.
In addition, fan selection often has to be performed with space and size limitations, sound considerations, maximum energy limits, high temperatures, specific sealing needs, ducting issues and many other factors. Illinois Blower engineers can help optimize every aspect, including selecting the right impeller design, identifying the most appropriate housings, and specifying the best materials.
Whatever the solution requires, Illinois Blower has more than 44 years of experience engineering custom fans that meet the most demanding requirements and operate in the most demanding conditions. Contact us today to talk about how we can help you best meet your industrial fan and blower needs.
Performance and fan efficiency are significantly impacted by the way speed, size and air density interact. Review our Fan Laws Cheat Sheet to see these crucial relationships summarized in one place.